Chapter 3. Oscillation
“Trigonometry is a sine of the times.”
— Anonymous
In Chapters 1 and 2, I carefully worked out an object-oriented structure to make something move on the screen, using the concept of a vector to represent position, velocity, and acceleration driven by forces in the environment. I could move straight from here into topics such as particle systems, steering forces, group behaviors, etc. If I did that, however, I’d skip an important area of mathematics that you’re going to need: trigonometry, or the mathematics of triangles, specifically right triangles.
Trigonometry is going to give you a lot of tools. You’ll get to think about angles and angular velocity and acceleration. Trig will teach you about the sine and cosine functions, which when used properly can yield a nice ease-in, ease-out wave pattern. It’s going to allow you to calculate more complex forces in an environment that involves angles, such as a pendulum swinging or a box sliding down an incline.
So this chapter is a bit of a mishmash. I’ll start with the basics of working with angles in p5.js and cover many trigonometric topics, tying it all into forces at the end. If I do it well, this will also pave the way for more sophisticated examples that require trig later in this book.
3.1 Angles
OK. Before you can do any of this stuff, I need to make sure you understand what it means to be an angle in p5.js. If you have experience with p5.js, you’ve undoubtedly encountered this issue while using the rotate() function to rotate and spin objects.
The first order of business is to cover radians and degrees. You’re probably familiar with the concept of an angle in degrees. A full rotation goes from 0 to 360 degrees. 90 degrees (a right angle) is 1/4th of 360, shown below as two perpendicular lines.

It’s probably more intuitive for you to think of angles in terms of degrees. For example, the square in Figure 3.2 is rotated 45 degrees around its center.

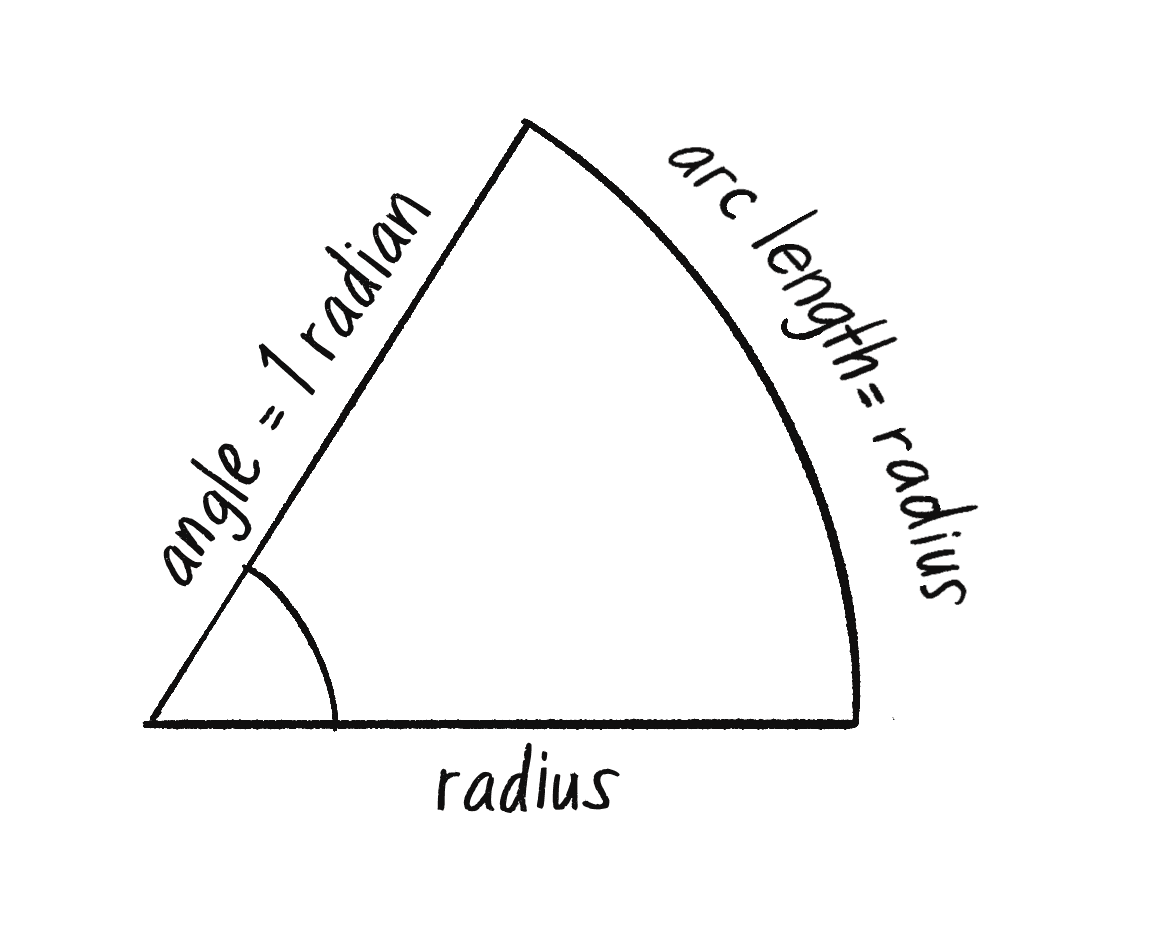
By default p5.js, however, considers angles to be specified in radians. A radian is a unit of measurement for angles defined by the ratio of the length of the arc of a circle to the radius of that circle. One radian is the angle at which that ratio equals one (see Figure 3.3). 180 degrees = PI radians, 360 degrees = 2*PI radians, 90 degrees = PI/2 radians, etc.
The formula to convert from degrees to radians is:
radians = 2 * PI * (degrees / 360)
Thankfully, if you prefer to think of angles in degrees you can call angleMode(DEGREES). p5.js also includes a convenience function radians() function to automatically converts values from degrees to radians as well as the constants PI and TWO_PI for access to these commonly used numbers (equivalent to 180 and 360 degrees, respectively). Here are two ways in p5.js to rotate a shape by 60 degrees.
While the above can be useful, for the purposes of this book I‘m going to always assume radians. In addition, if you are not familiar with how rotation is implemented in p5.js, I would suggest this transformations tutorial by Gene Kogan or this video series on transformations in p5.js.
What is PI?
The mathematical constant pi (or π) is a real number defined as the ratio of a circle’s circumference (the distance around the perimeter) to its diameter (a straight line that passes through the circle’s center). It is equal to approximately 3.14159 and can be accessed in p5 with the built-in variable PI.
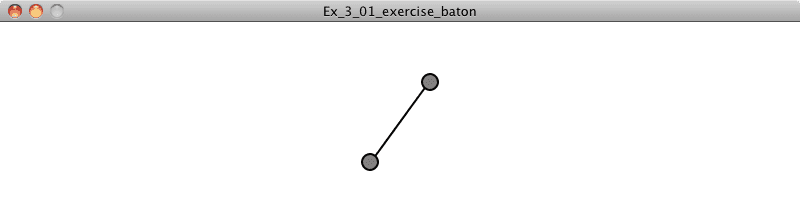
Exercise 3.1
Rotate a baton-like object (see below) around its center using translate() and rotate().
3.2 Angular Motion
Remember all this stuff?
The stuff we dedicated almost all of Chapters 1 and 2 to? Well, you can apply exactly the same logic to a rotating object.
In fact, the above is simpler than what I started with because an angle is a scalar quantity—a single number, not a vector!
Using the answer from Exercise 3.1 above, let’s say you wanted to rotate a baton in p5.js by some angle. The code might read:
translate(width/2, height/2);
rotate(angle);
line(-50, 0, 50, 0);
circle(50, 0, 8);
circle(-50, 0, 8);
Adding in the principles of motion, I can then write the following example (the solution to Exercise 3.1).
Example 3.1: Angular motion using rotate()

let angle = 0;
position
let aVelocity = 0;
Velocity
let aAcceleration = 0.001;
Acceleration
function setup() {
createCanvas(640, 360);
}
function draw() {
background(255);
fill(175);
stroke(0);
rectMode(CENTER);
translate(width/2, height/2);
rotate(angle);
line(-50, 0, 50, 0);
circle(50, 0, 8);
circle(-50, 0, 8);
aVelocity += aAcceleration;
Angular equivalent of velocity.add(acceleration);
angle += aVelocity;
Angular equivalent of position.add(velocity);
}
The baton starts onscreen with no rotation and then spins faster and faster as the angle of rotation accelerates.
Exercise 3.x-axis
Add an interaction to the spinning baton. How can you control the acceleration with the mouse? Can you introduce the idea of drag, decreasing the angular velocity over time so that it will always eventually come to rest?
This idea can be incorporated into the Mover class by adding new variables related to angular motion.
class Mover {
constructor(){
this.position = createVector();
this.velocity = createVector();
this.acceleration = createVector();
this.mass = 1.0;
this.angle = 0;
this.aVelocity = 0;
this.aAcceleration = 0;
}
}
And then in update(), position and angle are updated according to the same algorithm!
update() {
this.velocity.add(this.acceleration);
this.position.add(this.velocity);
Regular old-fashioned motion
this.aVelocity += this.aAcceleration;
this.angle += this.aVelocity;
Newfangled angular motion
this.acceleration.mult(0);
}
Of course, for any of this to matter, I also would need to rotate the object when displaying it. (I'll add drawing a line from the center to the edge of the circle so that rotation is viewabale. You could also use a shape other than a circle.)
display() {
stroke(0);
fill(175, 200);
rectMode(CENTER);
push();
push() and pop() are necessary so that the rotation of this shape doesn’t affect the rest of our world.
translate(this.position.x, this.position.y);
Set the origin at the shape’s position.
rotate(this.angle);
Rotate by the angle.
circle(0, 0, this.radius * 2);
line(0, 0, this.radius, 0);
pop();
}
Now, if you were to actually go ahead and run the above code, you wouldn’t see anything new. This is because the angular acceleration (this.aAcceleration = 0;) is initialized to zero. For the object to rotate, it needs a non-zero acceleration! Certainly, one option is to hard-code a number.
this.aAcceleration = 0.01;
However, you can produce a more interesting result by dynamically assigning an angular acceleration according to forces in the environment. Now, I could head far down this road and research modeling the physics of angular acceleration based on the concepts of torque and moment of inertia. Nevertheless, this level of simulation is beyond the scope of this book. (I will cover more about modeling angular acceleration with a pendulum later in this chapter, as well as look at how other physics libraries realistically models rotational motion in Chapter 5.)
For now, a quick and dirty solution will do. I can produce reasonable results by calculating angular acceleration as a function of the object’s acceleration vector. Here’s one such example:
this.aAcceleration = this.acceleration.x;
Yes, this is completely arbitrary. But it does do something. If the object is accelerating to the right, its angular rotation accelerates in a clockwise direction; acceleration to the left results in a counterclockwise rotation. Of course, it’s important to think about scale in this case. The x component of the acceleration vector might be a quantity that’s too large, causing the object to spin in a way that looks ridiculous or unrealistic. So dividing the x component by some value, or perhaps constraining the angular velocity to a reasonable range, could really help. Here’s the entire update() function with these tweaks added.
Example 3.2: Forces with (arbitrary) angular motion
update() {
this.velocity.add(this.acceleration);
this.position.add(this.velocity);
this.aAcceleration = this.acceleration.x / 10.0;
Calculate angular acceleration according to acceleration’s horizontal direction and magnitude.
this.aVelocity += this.aAcceleration;
this.aVelocity = constrain(this.aVelocity, -0.1, 0.1);
Use constrain() to ensure that angular velocity doesn’t spin out of control.
this.angle += this.aVelocity;
this.acceleration.mult(0);
}
Exercise 3.2
Step 1: Create a simulation where objects are shot out of a cannon. Each object should experience a sudden force when shot (just once) as well as gravity (always present).
Step 2: Add rotation to the object to model its spin as it is shot from the cannon. How realistic can you make it look?
3.3 Trigonometry
I think it may be time. I’ve discussed angles, I’ve spun a baton. It’s time for: sohcahtoa. Yes, sohcahtoa. This seemingly nonsensical word is actually the foundation for a lot of computer graphics work. A basic understanding of trigonometry is essential if you want to calculate an angle, figure out the distance between points, work with circles, arcs, or lines. And sohcahtoa is a mnemonic device (albeit a somewhat absurd one) for what the trigonometric functions sine, cosine, and tangent mean.

- soh: sine = opposite / hypotenuse
- cah: cosine = adjacent / hypotenuse
- toa: tangent = opposite / adjacent

Take a look at Figure 3.4 again. There’s no need to memorize it, but make sure you feel comfortable with it. Draw it again yourself. Now let’s draw it a slightly different way (Figure 3.5).
See how a right triangle is created from a vector? The vector arrow itself is the hypotenuse and the components of the vector (x and y) are the sides of the triangle. The angle is an additional means for specifying the vector’s direction (or “heading”).
Because the trigonometric functions establish a relationship between the components of a vector and its direction + magnitude, they will prove very useful throughout this book. I’ll begin by looking at an example that requires the tangent function.
3.4 Pointing in the Direction of Movement
Let’s go all the way back to Example 1.10, which features a Mover object accelerating towards the mouse.
You might notice that almost all of the shapes I’ve been drawing so far are circles. This is convenient for a number of reasons, one of which is that I don’t have to consider the question of rotation. Rotate a circle and, well, it looks exactly the same. However, there comes a time in all motion programmers’ lives when they want to draw something on the screen that points in the direction of movement. Perhaps you are drawing an ant, or a car, or a spaceship. And when I say “point in the direction of movement,” what I am really saying is “rotate according to the velocity vector.” Velocity is a vector, with an x and a y component, but to rotate in p5.js you need an angles. Let’s draw the trigonometry diagram once more, this time with an object’s velocity vector (Figure 3.6).
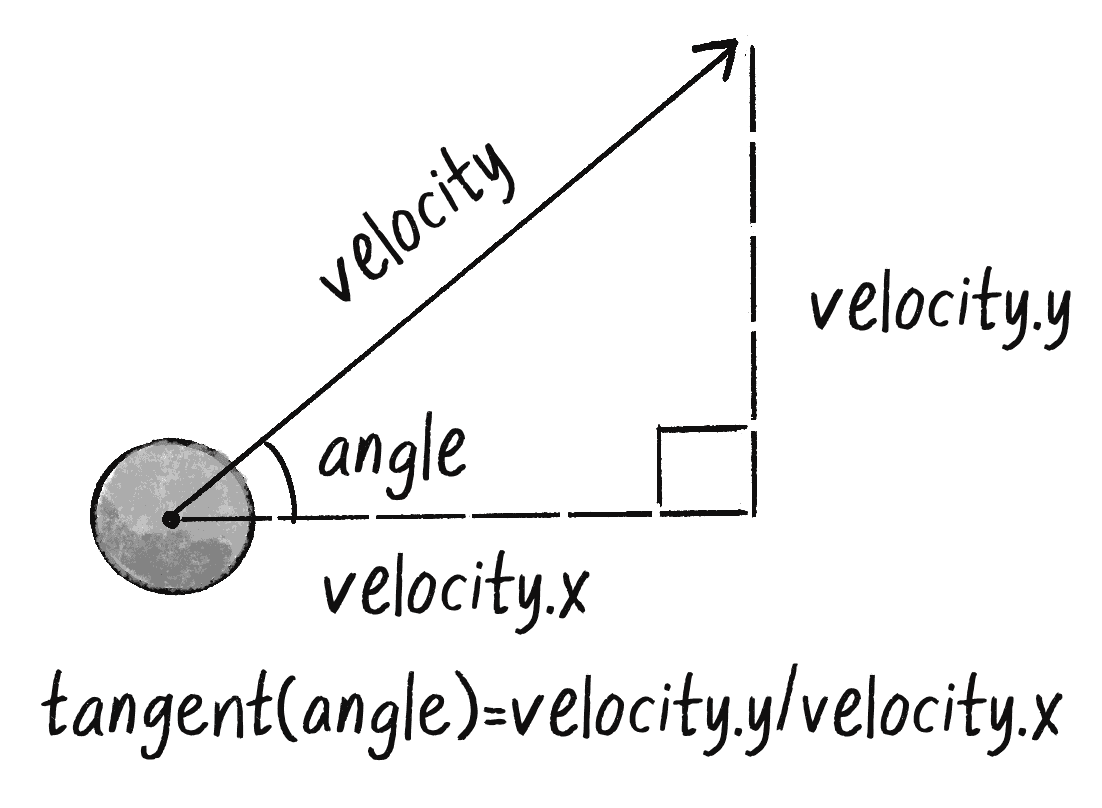
OK. I‘ve stayed the definition of tangent is:
The problem with the above is that while velocity is known, the angle of direction is not. I have to solve for that angle. This is where a special function known as inverse tangent comes in, also known to as arctangent or tan. (There is also an inverse sine and an inverse cosine.)
If the tangent of some value a equals some value b, then the inverse tangent of b equals a. For example:
| if | tangent(a) = b |
| then | a = arctangent(b) |
See how that is the inverse? The above now allows me to solve for the angle:
| if | tangent(angle) = velocity |
| then | angle = arctangent(velocity |
Now that I have the formula, let’s see where it should go in the mover’s display() function. Notice that in p5.js, the function for arctangent is called atan().
display() {
let angle = atan(this.velocity.y / this.velocity.x);
Solve for angle by using atan().
stroke(0);
fill(175);
push();
rectMode(CENTER);
translate(this.position.x, this.position.y);
rotate(angle);
Rotate according to that angle.
rect(0, 0, 30, 10);
pop();
}
Now the above code is pretty darn close, and almost works. There is a big problem, though. Consider the two velocity vectors depicted below.
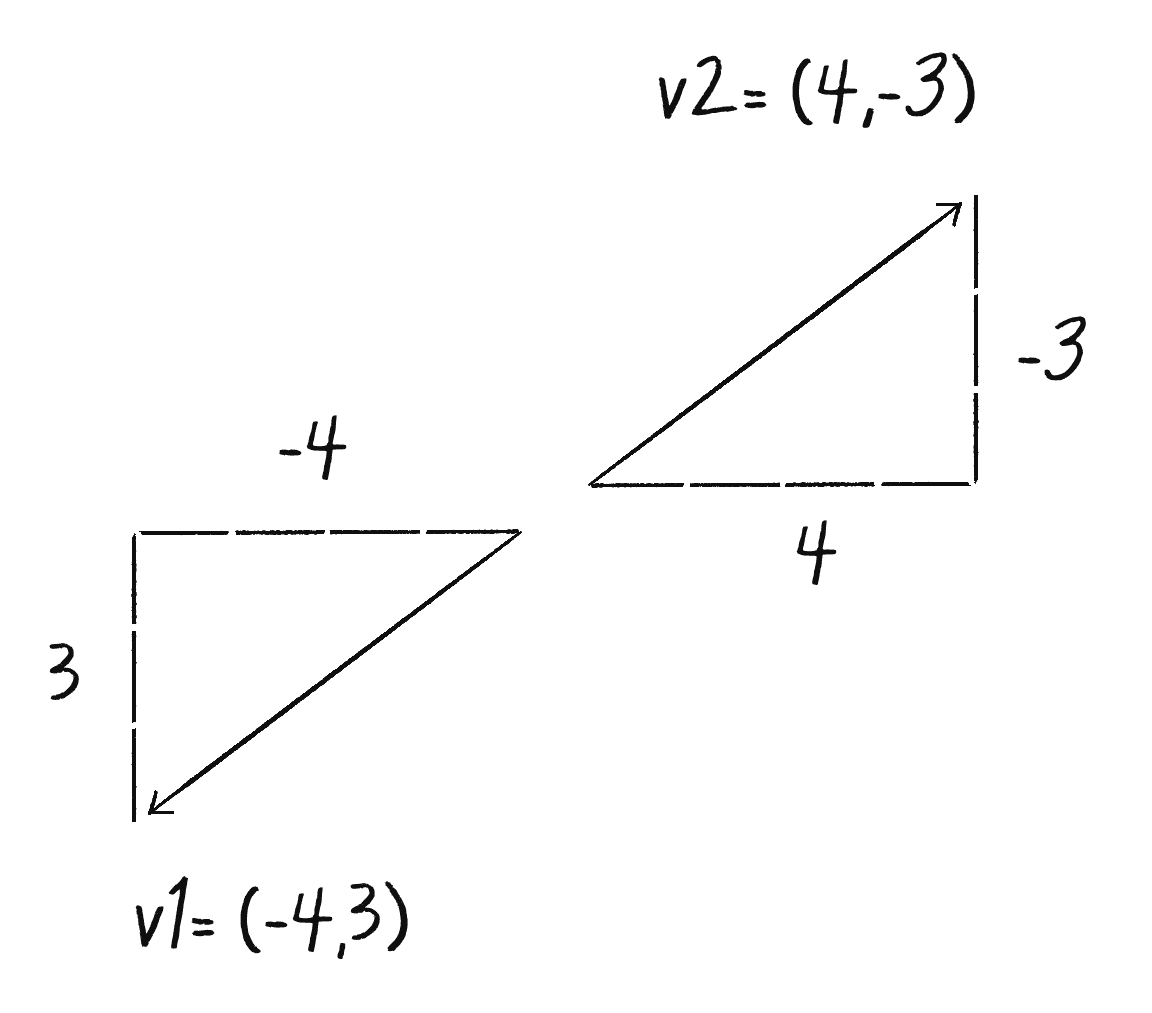
Though superficially similar, the two vectors point in quite different directions—opposite directions, in fact! However, if I were to apply the formula to solve for the angle to each vector…
…I get the same angle for each vector. This can’t be right for both; the vectors point in opposite directions! The thing is, this is a pretty common problem in computer graphics. Rather than using atan() along with a bunch of conditional statements to account for positive/negative scenarios, p5.js (along with pretty much all programming environments) has a nice function called atan2() that does it for you.
Example 3.3: Pointing in the direction of motion
display() {
let angle = atan2(this.velocity.y, this.velocity.x);
Using atan2() to account for all possible directions
stroke(0);
fill(175);
push();
rectMode(CENTER);
translate(this.position.x, this.position.y);
rotate(angle);
Rotate according to that angle.
rect(0, 0, 30, 10);
pop();
}
To simplify this even further, the p5.Vector class itself provides a function called heading(), which takes care of calling atan2() for you so you can get the 2D direction angle, in radians, for any p5.Vector.
let angle = this.velocity.heading();
The easiest way to do this!
Exercise 3.3
Create a simulation of a vehicle that you can drive around the screen using the arrow keys: left arrow accelerates the car to the left, right to the right. The car should point in the direction in which it is currently moving.
3.5 Polar vs. Cartesian Coordinates
Any time you display a shape in p5, you have to specify a pixel position, a set of x and y coordinates. These coordinates are known as Cartesian coordinates, named for René Descartes, the French mathematician who developed the ideas behind Cartesian space.
Another useful coordinate system known as polar coordinates describes a point in space as an angle of rotation around the origin and a radius from the origin. Thinking about this in terms of a vector:
Cartesian coordinate—the x,y components of a vectorPolar coordinate—the magnitude (length) and direction (angle) of a vector
p5.js’s drawing functions, however, don’t understand polar coordinates. Whenever you want to display something, you have to specify positions as (x,y) Cartesian coordinates. However, sometimes it is much more convenient to think in polar coordinates when designing. Happily for you, with trigonometry you can convert back and forth between Polar and Cartesian, designing with whatever coordinate system you have in mind but always drawing with Cartesian coordinates.
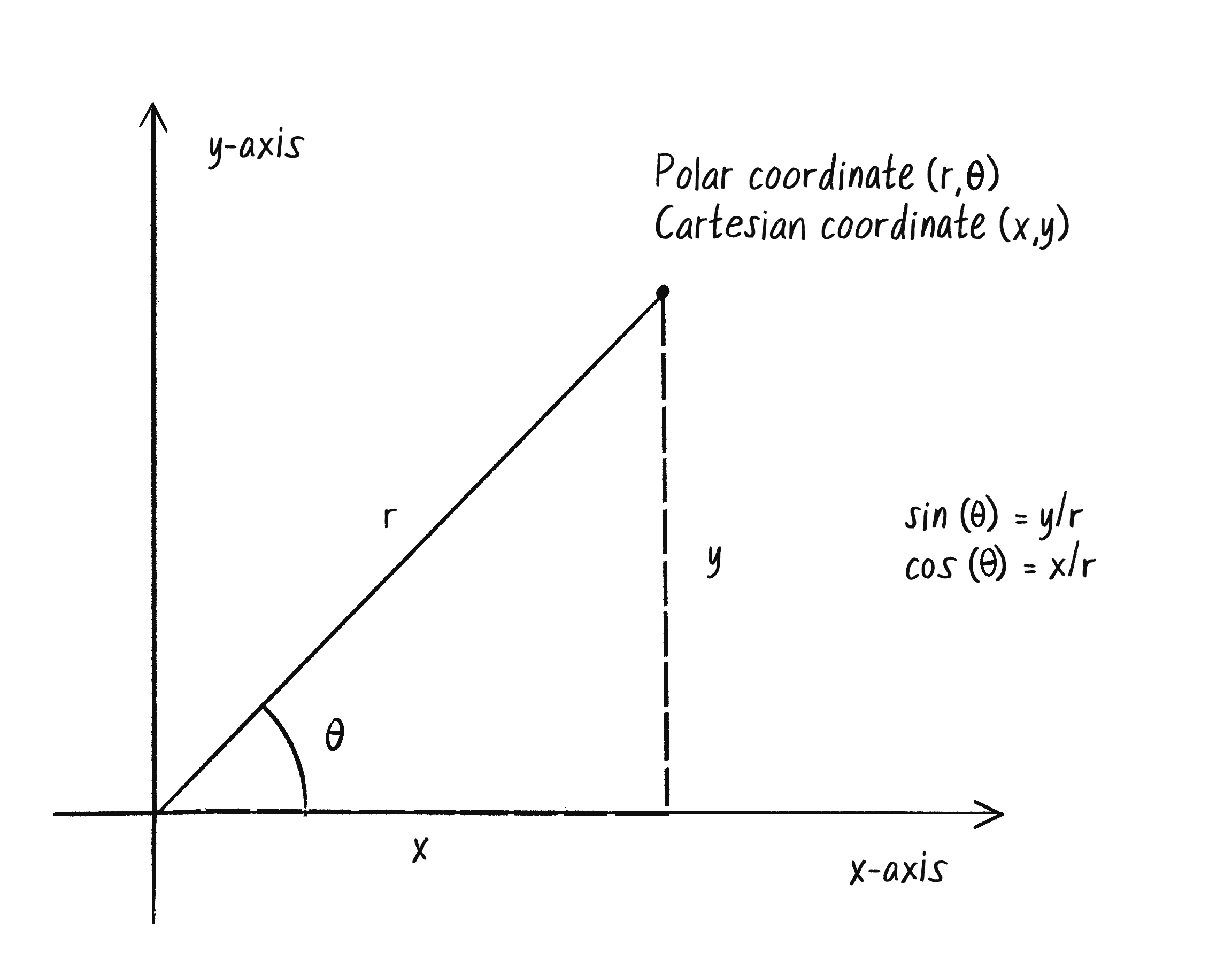
For example, if r is 75 and theta is 45 degrees (or PI/4 radians), x and y can be computed as follow. (The functions for sine and cosine in p5.js are sin() and cos(), respectively. They each take one argument, a number representing an angle.)
let r = 75;
let theta = PI / 4;
let x = r * cos(theta);
let y = r * sin(theta);
Converting from polar (r,theta) to Cartesian (x,y)
This type of conversion can be useful in certain applications. For example, to move a shape along a circular path using Cartesian coordinates is not so easy. With polar coordinates, on the other hand, it’s simple: increment the angle!
Here’s how it is done with global variables r and theta.
Example 3.4: Polar to Cartesian

let r = 75;
let theta = 0;
function setup() {
createCanvas(640, 360);
background(255);
}
function draw() {
let x = r * cos(theta);
let y = r * sin(theta);
Polar coordinates (r,theta) are converted to Cartesian (x,y) for use in the circle() function.
noStroke();
fill(0);
circle(x + width/2, y + height/2, 16);
theta += 0.01;
}
Exercise 3.4
Using Example 3.4 as a basis, draw a spiral path. Start in the center and move outwards. Note that this can be done by only changing one line of code and adding one line of code!

Exercise 3.5
Simulate the spaceship in the game Asteroids. In case you aren’t familiar with Asteroids, here is a brief description: A spaceship (represented as a triangle) floats in two dimensional space. The left arrow key turns the spaceship counterclockwise, the right arrow key, clockwise. The z key applies a “thrust” force in the direction the spaceship is pointing.
3.6 Oscillation Amplitude and Period
Are you amazed yet? I’ve demonstrated some pretty great uses of tangent (for finding the angle of a vector) and sine and cosine (for converting from polar to Cartesian coordinates). I could stop right here and be satisfied. But I’m not going to. This is only the beginning. What sine and cosine can do for you goes beyond mathematical formulas and right triangles.
Let’s take a look at a graph of the sine function, where y = sine(x).
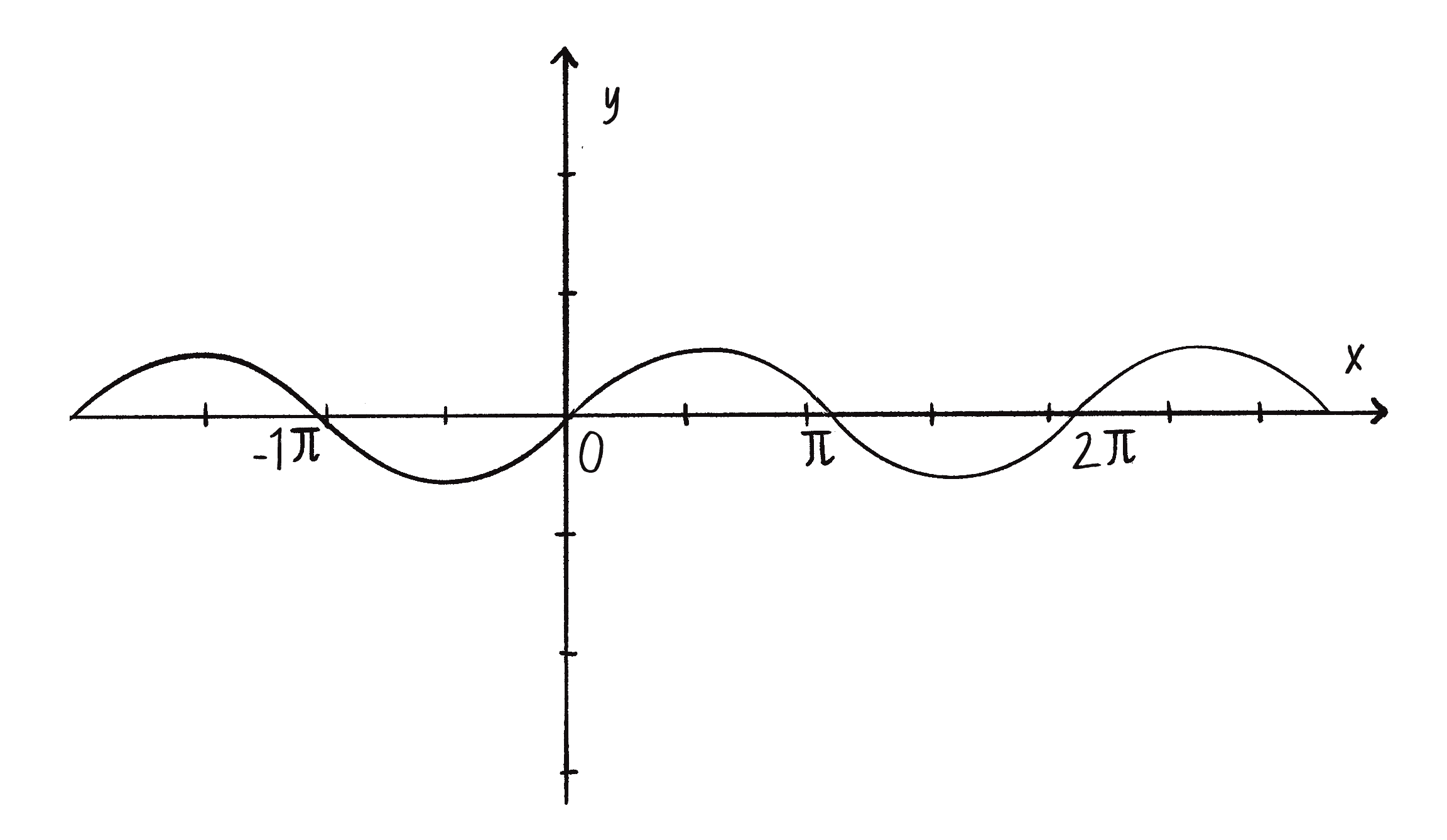
You’ll notice that the output of the sine function is a smooth curve alternating between −1 and 1. This type of a behavior is known as oscillation, a periodic movement between two points. Plucking a guitar string, swinging a pendulum, bouncing on a pogo stick—these are all examples of oscillating motion.
And so you will happily discover that you can simulate oscillation in a p5.js sketch by assigning the output of the sine function to an object’s position. Note that this will follow the same methodology we applied to Perlin noise in the Introduction.
Let’s begin with a really basic scenario. I want a circle to oscillate from the left side to the right side of a p5.js canvas.
This is what is known as simple harmonic motion (or, to be fancier, “the periodic sinusoidal oscillation of an object”). It’s going to be a simple program to write, but before I get into the code, I should familiarize you with some of the terminology of oscillation (and waves).
Simple harmonic motion can be expressed as any position (in this case, the x position) as a function of time, with the following two elements:
- Amplitude: The distance from the center of motion to either extreme
- Period: The amount of time it takes for one complete cycle of motion
The graph of sine (Figure 3.9) shows that the amplitude is 1 and the period is TWO_PI; the output of sine never rises above 1 or below -1; and every TWO_PI radians (or 360 degrees) the wave pattern repeats.
Now, in a p5.js world, what is amplitude and what is period? Amplitude can be measured rather easily in pixels. In the case of a window 200 pixels wide, I might choose to oscillate from the center 100 pixels to the right and 100 pixels to the left. Therefore:
let amplitude = 100;
The amplitude is measured in pixels.
Period is the amount of time it takes for one cycle, but what is time in a p5.js sketch? I mean, certainly I could say I want the circle to oscillate every three seconds. And I could track the milliseconds—using millis() —in p5.js and come up with an elaborate algorithm for oscillating an object according to real-world time. But for what I‘m trying to accomplish here, real-world time doesn’t really matter. The useful measure of time in p5.js is in frames. The oscillating motion should repeat every 30 frames, or 50 frames, or 1000 frames, etc.
let period = 120;
Period is measured in frames (the unit of time for animation).
Once I have the amplitude and period, it’s time to write a formula to calculate x as a function of time, which I‘ve established as the current frame count.
let x = amplitude * sin(TWO_PI * frameCount / period);
Let’s dissect the formula a bit more and try to understand each component. The first is probably the easiest. Whatever comes out of the sine function is multiplied by amplitude. The output of the sine function oscillates between -1 and 1. If you take that value and multiply it by amplitude then you’ll get the desired result: a value oscillating between -amplitude and amplitude. (Note: this is also a place where we could use p5.js’s map() function to map the output of sine to a custom range.)
Now, let’s look at what is inside the sine function:
TWO_PI * frameCount / period
What’s going on here? Let’s start with what you know. I‘ve explained that sine will repeat every 2*PI radians—i.e. it will start at 0 and repeat at 2*PI, 4*PI, 6*PI, etc. If the period is 120, then I want the oscillating motion to repeat when the frameCount is at 120 frames, 240 frames, 360 frames, etc. frameCount is really the only value changing here; it starts at 0 and counts upward. Let’s take a look at what the formula yields as frameCount increases.
| frameCount | frameCount / period | TWO_PI * frameCount / period |
|---|---|---|
| 0 | 0 | 0 |
| 60 | 0.5 | PI |
| 120 | 1 | TWO_PI |
| 240 | 2 | 2 * TWO_PI (or 4 * PI) |
| etc. |
frameCount divided by period tells you how many cycles have been completed—is the wave halfway through the first cycle? Have two cycles completed? By multiplying that number by TWO_PI, I get the desired result, since TWO_PI is the number of radians required for sine (or cosine) to complete one full cycle.
Wrapping this all up, here’s the p5.js example that oscillates the x position of a circle with an amplitude of 100 pixels and a period of 120 frames.
Example 3.5: Simple Harmonic Motion
function setup() {
createCanvas(640, 360);
}
function draw() {
background(255);
let period = 120;
let amplitude = 100;
let x = amplitude * sin(TWO_PI * frameCount / period);
Calculating horizontal position according to the formula for simple harmonic motion
stroke(0);
fill(175);
translate(width/2, height/2);
line(0, 0, x, 0);
circle(x, 0, 20);
}
It’s also worth mentioning the term frequency: the number of cycles per time unit. Frequency is equal to 1 divided by period. If the period is 120 frames, then only 1/120th of a cycle is completed in one frame, and so frequency = 1/120. In the above example, I chose to define the rate of oscillation in terms of period and therefore did not need a variable for frequency.
Exercise 3.6
Using the sine function, create a simulation of a weight (sometimes referred to as a “bob”) that hangs from a spring from the top of the window. Use the map() function to calculate the vertical position of the bob. Later in this chapter, I’ll demonstrate how to recreate this same simulation by modeling the forces of a spring according to Hooke’s law.
3.7 Oscillation with Angular Velocity
An understanding of the concepts of oscillation, amplitude, and frequency/period is often required in the course of simulating real-world behaviors. However, there is a slightly easier way to rewrite the above example with the same result. Let’s take one more look at the oscillation formula:
let x = amplitude * sin(TWO_PI * frameCount / period);
Below I‘ll rewrite it a slightly different way:
const x = amplitude * sin ( some value that increments slowly );
If you care about precisely defining the period of oscillation in terms of frames of animation, you might need the formula the way I first wrote it, but I could just as easily rewrite the example using the concept of angular velocity (and acceleration) from section 3.2. Assuming:
let angle = 0;
let aVelocity = 0.05;
in draw(), we can simply say:
angle += aVelocity;
let x = amplitude * sin(angle);
angle is “some value that increments slowly.”
Example 3.6: Simple Harmonic Motion II
let angle = 0;
let aVelocity = 0.05;
function setup() {
createCanvas(640, 360);
}
function draw() {
background(255);
let amplitude = 100;
let x = amplitude * sin(angle);
angle += aVelocity;
Using the concept of angular velocity to increment an angle variable
ellipseMode(CENTER);
stroke(0);
fill(175);
translate(width/2, height/2);
line(0, 0, x, 0);
circle(x, 0, 20);
}
Just because I’m not referencing it directly doesn’t mean that I’ve eliminated the concept of period. After all, the greater the angular velocity, the faster the circle will oscillate (therefore lowering the period). In fact, the number of draw() loops to add up the angular velocity all the way to TWO_PI is the period or:
Let’s expand this example a bit more and create an Oscillator class. And let’s assume I want the oscillation to happen along both the x-axis (as above) and the y-axis. To do this, I’ll need two angles, two angular velocities, and two amplitudes (one for each axis). Another perfect opportunity for createVector()!
Example 3.7: Oscillator objects
class Oscillator {
constructor() {
this.angle = createVector();
this.velocity = createVector(random(-0.05, 0.05),random(-0.05, 0.05));
Using a p5.Vector to track two angles!
this.amplitude = createVector(random(width/2), random(height/2));
Random velocities and amplitudes
}
oscillate() {
this.angle.add(this.velocity);
}
display() {
let x = sin(this.angle.x) * this.amplitude.x;
Oscillating on the x-axis
let y = sin(this.angle.y) * this.amplitude.y;
Oscillating on the y-axis
push();
translate(width/2, height/2);
stroke(0);
fill(175);
line(0, 0, x, y);
circle(x, y, 16);
pop();
}
}
Drawing the Oscillator as a line connecting a circle
Exercise 3.7
Try initializing each Oscillator object with velocities and amplitudes that are not random to create some sort of regular pattern. Can you make the oscillators appear to be the legs of an insect-like creature?
Exercise 3.8
Incorporate angular acceleration into the Oscillator object.
3.8 Waves
If you’re saying to yourself, “Um, this is all great and everything, but what I really want is to draw a wave,” well, then, the time has come. When you oscillate a single circle up and down according to the sine function, what you are doing is equivalent to simulating a single point along the x-axis of a wave pattern. With a little panache and a for loop, you can place a whole bunch of these oscillating circles next to each other.
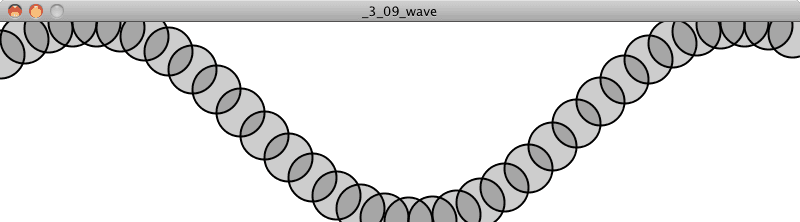
This wavy pattern could be used in the design of the body or appendages of a creature, as well as to simulate a soft surface (such as water).
Here, the same questions of amplitude (height of pattern) and period apply. Instead of period referring to time, however, since the example renders the full wave, I‘ll refer to period as the width (in pixels) of a full wave cycle. And just as with simple oscillation, you have the option of computing the wave pattern according to a precise period or following the model of angular velocity.
Let’s go with the simpler case, angular velocity. I know I need to start with an angle, an angular velocity, and an amplitude:
let angle = 0;
let angleVel = 0.2;
let amplitude = 100;
Then I’m going to loop through all of the x values for each point on the wave. I’ll pick every 24 pixels for now and follow these three steps:
- Calculate the y position according to amplitude and sine of the angle.
- Draw a circle at the (x,y) position.
- Increment the angle according to angular velocity.
for (let x = 0; x <= width; x += 24) {
let y = amplitude * sin(angle);
1) Calculate the y position according to amplitude and sine of the angle.
circle(x, y + height/2, 48);
2) Draw a circle at the (x,y) position.
angle += angleVel;
}
3) Increment the angle according to angular velocity.
Here are the results with different values for angleVel:
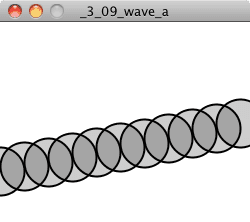
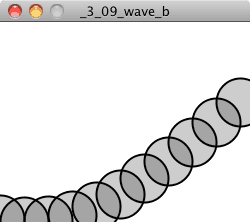
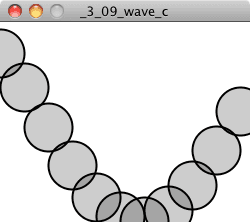
Although I’m not precisely computing the period of the wave, the higher the angular velocity, the shorter the period. It’s also worth noting that as the period decreases, it becomes more difficult to make out the wave itself since the distance between the individual points increases. One option to improve the visual quality is to use beginShape() and endShape() to connect the points with a line.
Example 3.8: Static wave drawn as a continuous line
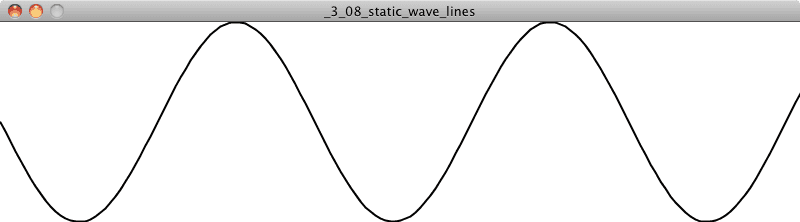
let angle = 0;
let angleVel = 0.2;
let amplitude = 100;
function setup(){
createCanvas(640, 360);
background(255);
stroke(0);
strokeWeight(2);
noFill();
beginShape();
for (let x = 0; x <= width; x += 5) {
let y = map(sin(angle), -1, 1, 0, height);
Here’s an example of using the map() function instead.
vertex(x, y);
angle += angleVel;
}
endShape();
}
With beginShape() and endShape(), you call vertex() to set all the vertices of your shape.
You may have noticed that the above example is static. The wave never changes, never undulates. This additional step is a bit tricky. Your first instinct might be to say: “Hey, no problem, I’ll just let theta be a global variable and increment it from one cycle through draw() to another.”
While it’s a nice thought, it doesn’t work. If you look at the wave, the righthand edge doesn’t match the lefthand; where it ends in one cycle of draw() can’t be where it starts in the next. Instead, what you need to do is have a variable dedicated entirely to tracking the starting angle value of the wave. This angle (which I’ll call startAngle) increments with its own angular velocity.
Example 3.9: The Wave
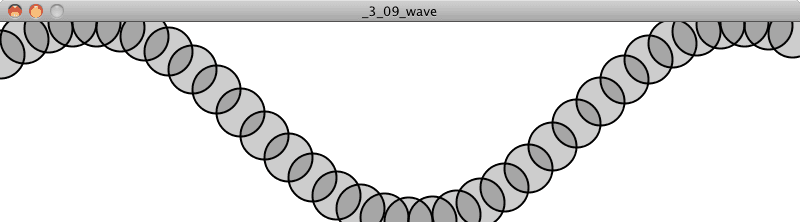
let startAngle = 0;
let angleVel = 0.1;
function setup() {
createCanvas(640, 360);
}
function draw() {
background(255);
let angle = startAngle;
startAngle += 0.02;
In order to move the wave, we start at a different theta value each frame.
for (let x = 0; x <= width; x += 24) {
const y = map(sin(angle), -1, 1, 0, height);
stroke(0);
fill(0, 50);
circle(x, y, 48);
angle += angleVel;
}
}
Exercise 3.9
Try using the Perlin noise function instead of sine or cosine with the above example.
Exercise 3.10
Encapsulate the above examples into a Wave class and create a sketch that displays two waves (with different amplitudes/periods) as in the screenshot below. Move beyond plain circles and lines and try visualizing the wave in a more creative way.
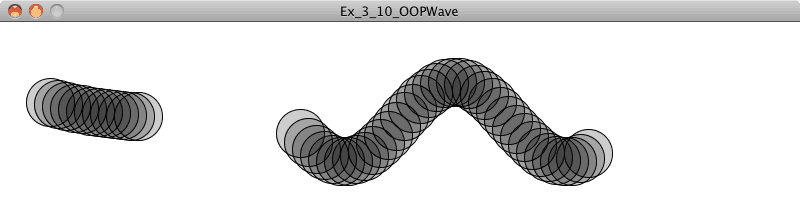
Exercise 3.11
More complex waves can be produced by the summing multiple waves together. Create a sketch that implements this, as in the screenshot below.

3.9 Trigonometry and Forces: The Pendulum
Do you miss Newton’s laws of motion? I know I sure do. Well, lucky for you, it’s time to bring it all back home. After all, it’s been nice learning about triangles and tangents and waves, but really, the core of this book is about simulating the physics of moving bodies. Let’s take a look at how trigonometry can help with this pursuit.
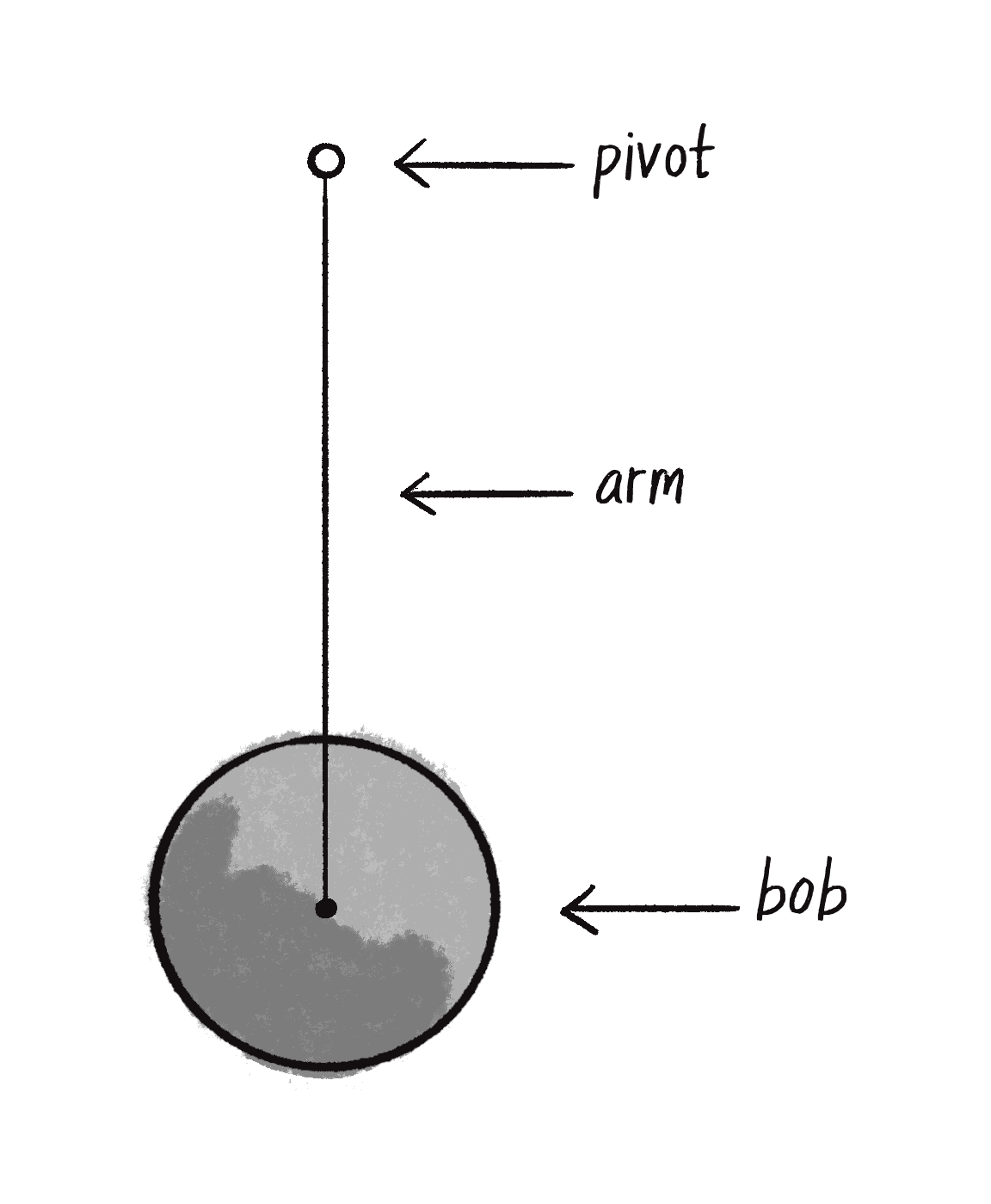
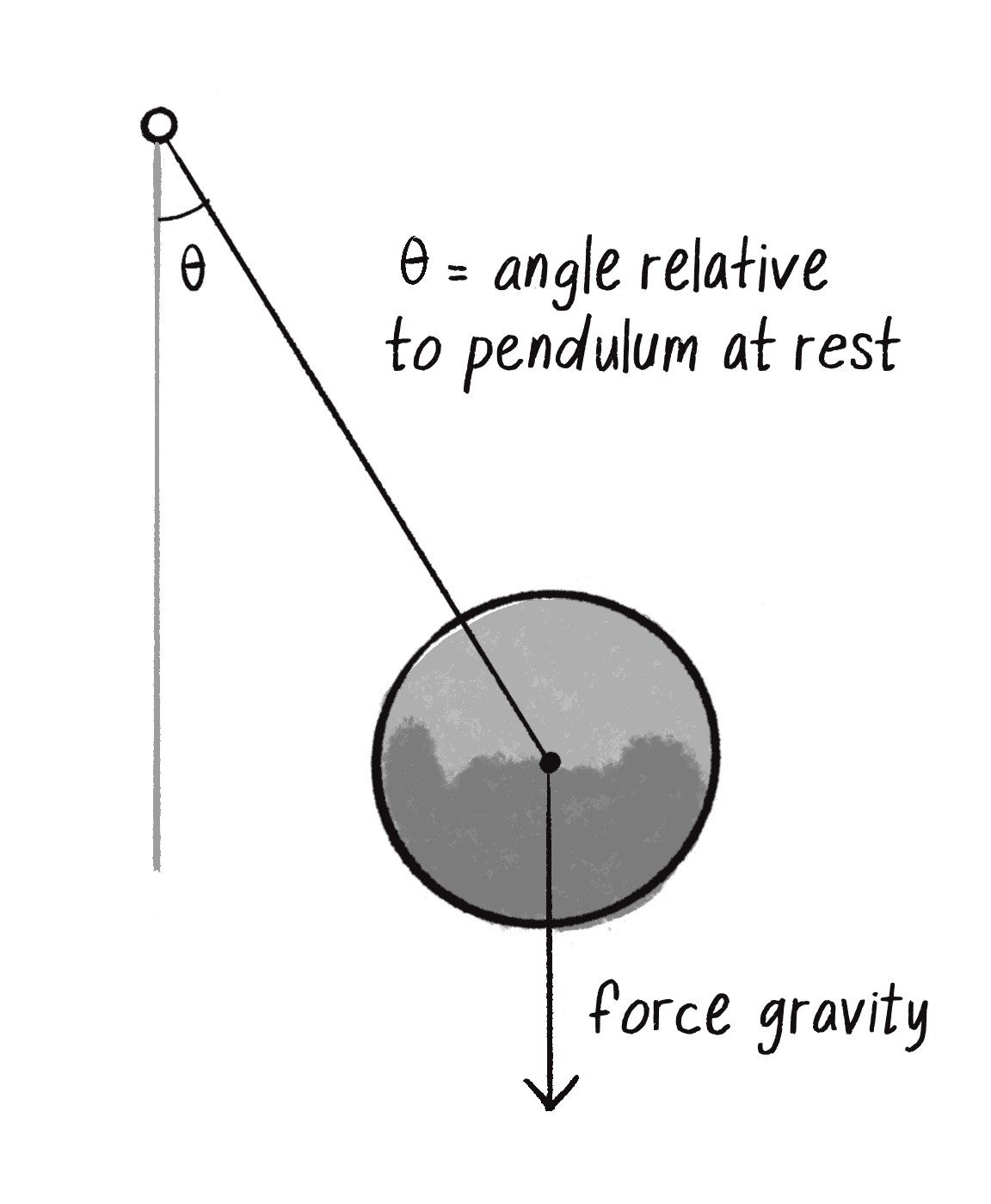
A pendulum is a bob suspended from a pivot. A real-world pendulum would live in a 3D space, but I’m going to look at a simpler scenario, a pendulum in a 2D space—a p5 canvas (see Figure 3.10).
In Chapter 2, I discussed how a force (such as the force of gravity in Figure 3.11) causes an object to accelerate. or . In this case, however, the pendulum bob doesn’t fall to the ground because it is attached by an arm to the pivot point. And so, in order to determine its angular acceleration, I not only need to look at the force of gravity vector, but also the component of that vector relative to the angle of the pendulum’s arm (which itself is an angle relative to a pendulum at rest).
In the above case, since the pendulum’s arm is of fixed length, the only variable in the scenario is the angle. I am going to simulate the pendulum’s motion through the use of angular velocity and acceleration. The angular acceleration will be calculated using Newton’s second law with a little trigonometry twist.
Let’s zoom in on the right triangle from the pendulum diagram.

You can see that the force of the pendulum (Fp) should point perpendicular to the arm of the pendulum in the direction that the pendulum is swinging. After all, if there were no arm, the bob would fall straight down. It’s the tension force of the arm that keeps the bob accelerating towards the pendulum’s rest state. Since the force of gravity (Fg) points downward, by making a right triangle out of these two vectors, you’ll see something quite magnificent. The force of gravity becomes the hypotenuse of a right triangle which can be separated into two components, one of which represents the force of the pendulum. Since sine equals opposite over hypotenuse, you‘ll then have:
Therefore:
Lest you forget, I’ve been doing all of this with a single question in mind: What is the angular acceleration of the pendulum? Once I have the angular acceleration, I’ll be able to apply the rules of motion to find the new angle for the pendulum.
The good news is Newton’s second law states that there is a relationship between force and acceleration, namely F = M * A, or A = F / M. So if the force of the pendulum is equal to the force of gravity times sine of the angle, then:
This is a good time for a reminder that I’m a p5.js coder and not a physicist. Yes, I know that the acceleration due to gravity on earth is 9.8 meters per second squared. But this number isn’t relevant here. What I have is just an arbitrary constant (I’ll call it gravity), one that we can use to scale the acceleration to something that feels right.
Amazing. After all that, the formula is so simple. You might be wondering, why bother going through the derivation at all? I mean, learning is great and all, but I could have easily just said, "Hey, the angular acceleration of a pendulum is some constant times the sine of the angle." This is just another moment for me to emphasize that the purpose of the book is not to learn how pendulums swing or gravity works. The point is to think creatively about how things can move about the screen in a computationally based graphics system. The pendulum is just a case study. If you can understand the approach to programming a pendulum, then however you choose to design your onscreen world, you can apply the same techniques.
Of course, I’m not finished yet. I may be happy with the simple, elegant formula, but I still have to apply it in code. This is most definitely a good time to practice some object-oriented programming skills and create a Pendulum class. Let’s think about all the properties I’ve mentioned in the pendulum discussion that the class will need:
- arm length
- angle
- angular velocity
- angular acceleration
class Pendulum {
constructor(){
this.r = ????;
Length of arm
this.angle = ????;
Pendulum arm angle
this.aVelocity = ????;
Angular velocity
this.aAcceleration = ????;
}
Angular acceleration
I’ll also need to write a function update() to update the pendulum’s angle according to the formula…
update() {
let gravity = 0.4;
Arbitrary constant
this.aAcceleration = -1 * gravity * sin(this.angle);
Calculate acceleration according to our formula.
this.aVelocity += this.aAcceleration;
Increment velocity.
this.angle += this.aVelocity;
Increment angle.
}
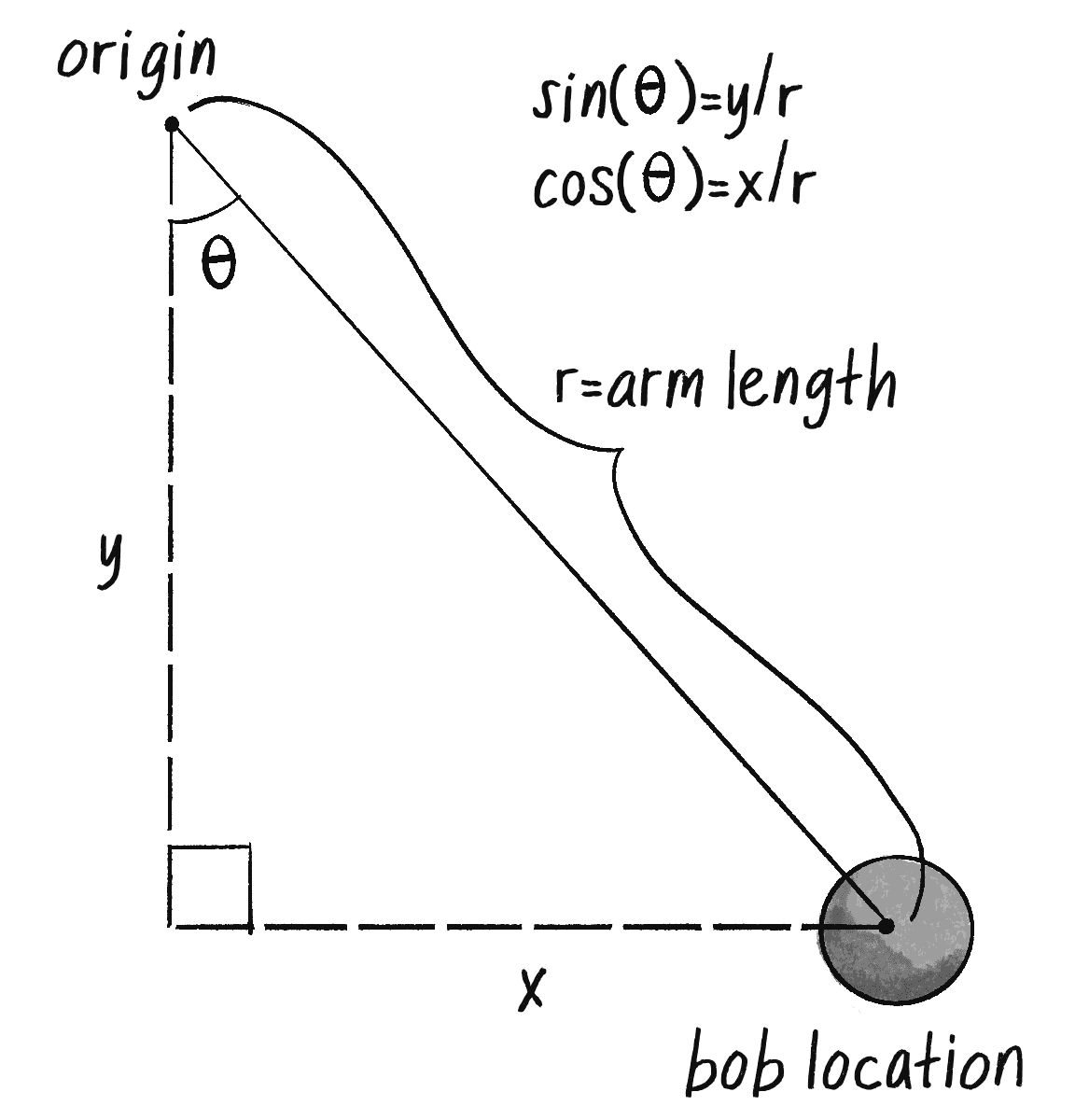
...as well as a function display() to draw the pendulum on the canvas. This begs the question: “Um, where do you draw the pendulum?” I know the angle and the arm length, but how do I calculate the x,y (Cartesian!) coordinates for both the pendulum’s pivot point (let’s call it origin) and bob position (let’s call it position)? This may be getting a little tiresome, but the answer, yet again, is trigonometry.
The origin is just something made up, as is the arm length. Let’s say:
this.origin = createVector(100, 10);
this.r = 125;
I’ve got the current angle stored in the variable angle. So relative to the origin, the pendulum’s position is a polar coordinate: (r,angle). And I need it to be Cartesian. Luckily, I just spent some time (section 3.5) deriving the formula for converting from polar to Cartesian. And so:
let position = createVector(r * sin(this.angle), r * cos(this.angle));
Note, however that sin(angle) is used for the x-value and cos(angle) for the y. This is the opposite of the formula established earlier in Chapter 3. The reason for this is that I am looking for the top angle of the right-triangle pointing down as depicted in Figure 3.13.
Since the position is relative to wherever the origin happens to be, I can just add origin to the position vector:
this.position.add(this.origin);
And all that remains is the little matter of drawing a line and circle (you should be more creative, of course).
stroke(0);
fill(175);
line(this.origin.x, this.origin.y, this.position.x, this.position.y);
circle(this.position.x, this.position.y, 16);
Before I put everything together, there’s one last little detail I neglected to mention. Let’s think about the pendulum arm for a moment. Is it a metal rod? A string? A rubber band? How is it attached to the pivot point? How long is it? What is its mass? Is it a windy day? There are a lot of questions that I could continue to ask that would affect the simulation. I choose to live, however, in a fantasy world, one where the pendulum’s arm is some idealized rod that never bends and the mass of the bob is concentrated in a single, infinitesimally small point. Nevertheless, even though I don’t want to worry myself with all of these questions, I should add one more variable to the calculation of angular acceleration. To keep things simple, in the derivation of the pendulum’s acceleration, I assumed that the length of the pendulum’s arm is 1. In truth, the length of the pendulum’s arm affects the acceleration greatly: the longer the arm, the slower the acceleration. To simulate a pendulum more accurately, I suggest dividing by that length, in this case r. For a more involved explanation, visit The Simple Pendulum website.
this.aAcceleration = (-1 * G * sin(this.angle)) / r;
Finally, a real-world pendulum is going to experience some amount of friction (at the pivot point) and air resistance. With the code as is, the pendulum would swing forever, so to make it more realistic I can use a “damping” trick. I say trick because rather than model the resistance forces with some degree of accuracy (as I did in Chapter 2), I can achieve a similar result by reducing the angular velocity during each cycle. The following code reduces the velocity by 1% (or multiplies it by 99%) during each frame of animation:
this.aVelocity *= 0.99;
Putting everything together, I have the following example (with the pendulum beginning at a 45-degree angle).
Example 3.10: Swinging pendulum

let pendulum;
function setup() {
createCanvas(640, 360);
pendulum = new Pendulum(width/2, 10, 125);
We make a new Pendulum object with an origin position and arm length.
}
function draw() {
background(255);
pendulum.update();
pendulum.display();
}
class Pendulum {
constructor(x, y, r) {
this.origin = createVector(x, y); // position of arm origin
this.position = createVector(); // position of bob
this.r = r; // Length of arm
this.angle = PI / 4; // Pendulum arm angle
this.aVelocity = 0; // Angle velocity
this.aAcceleration = 0; // Angle acceleration
this.damping = 0.995; // Arbitrary damping
Many, many variables to keep track of the Pendulum’s various properties
}
update() {
lete gravity = 0.4;
this.aAcceleration = (-1 * gravity / this.r) * sin(this.angle);
Formula we worked out for angular acceleration
this.aVelocity += this.aAcceleration;
this.angle += this.aVelocity;
Standard angular motion algorithm
this.aVelocity *= this.damping;
}
display() {
Apply some damping.
this.position.set(this.r * sin(this.angle), this.r * cos(this.angle));
Where is the bob relative to the origin? Polar to Cartesian coordinates will tell us!
this.position.add(this.origin);
stroke(0);
line(this.origin.x, this.origin.y, this.position.x, this.position.y);
The arm
fill(175);
circle(this.position.x, this.position.y, 16);
The bob
}
}
(Note that the version of the example posted on the website has additional code to allow the user to grab the pendulum and swing it with the mouse.)
Exercise 3.12
String together a series of pendulums so that the endpoint of one is the origin point of another. Note that doing this may produce intriguing results but will be wildly inaccurate physically. Simulating an actual double pendulum involves sophisticated equations, which you can read about here: http://scienceworld.wolfram.com/physics/DoublePendulum.html.
Exercise 3.13
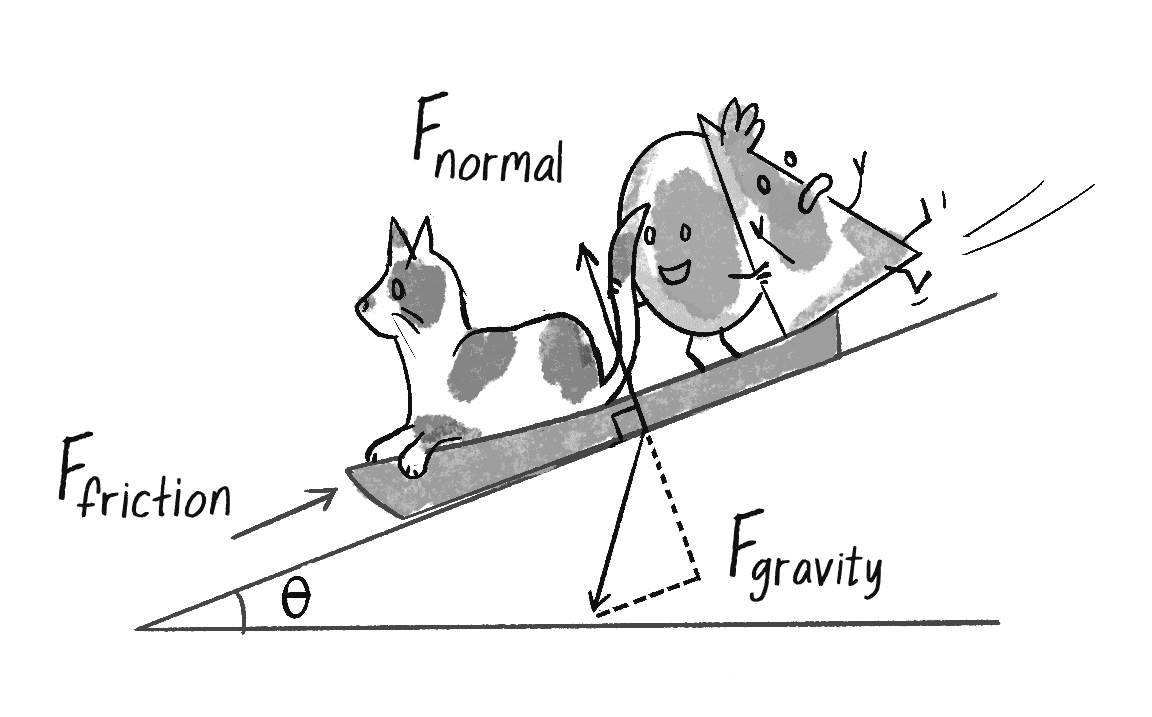
Using trigonometry, what is the magnitude of the normal force in the illustration on the right (the force to the incline on which the sled rests)? Note that, as indicated, the “normal” force is a component of the force of gravity. [NOTE: Add some tips about drawing over the diagram, looking for the right angle]

Exercise 3.14
Create an example that simulates a box sliding down the incline with friction. Note that the magnitude of the friction force is equal to the normal force.
3.10 Spring Forces
In section 3.6, I looked at modeling simple harmonic motion by mapping the sine wave to a pixel range. Exercise 3.6 asked you to use this technique to create a simulation of a bob hanging from a spring. While using the sin() function is a quick-and-dirty, one-line-of-code way of getting such a result, it won’t do if what you really want is to have a bob hanging from a spring in a two-dimensional space that responds to other forces in the environment (wind, gravity, etc.) To accomplish a simulation like this (one that is identical to the pendulum example, only now the arm is a springy connection), you need to model the forces of a spring using vectors.
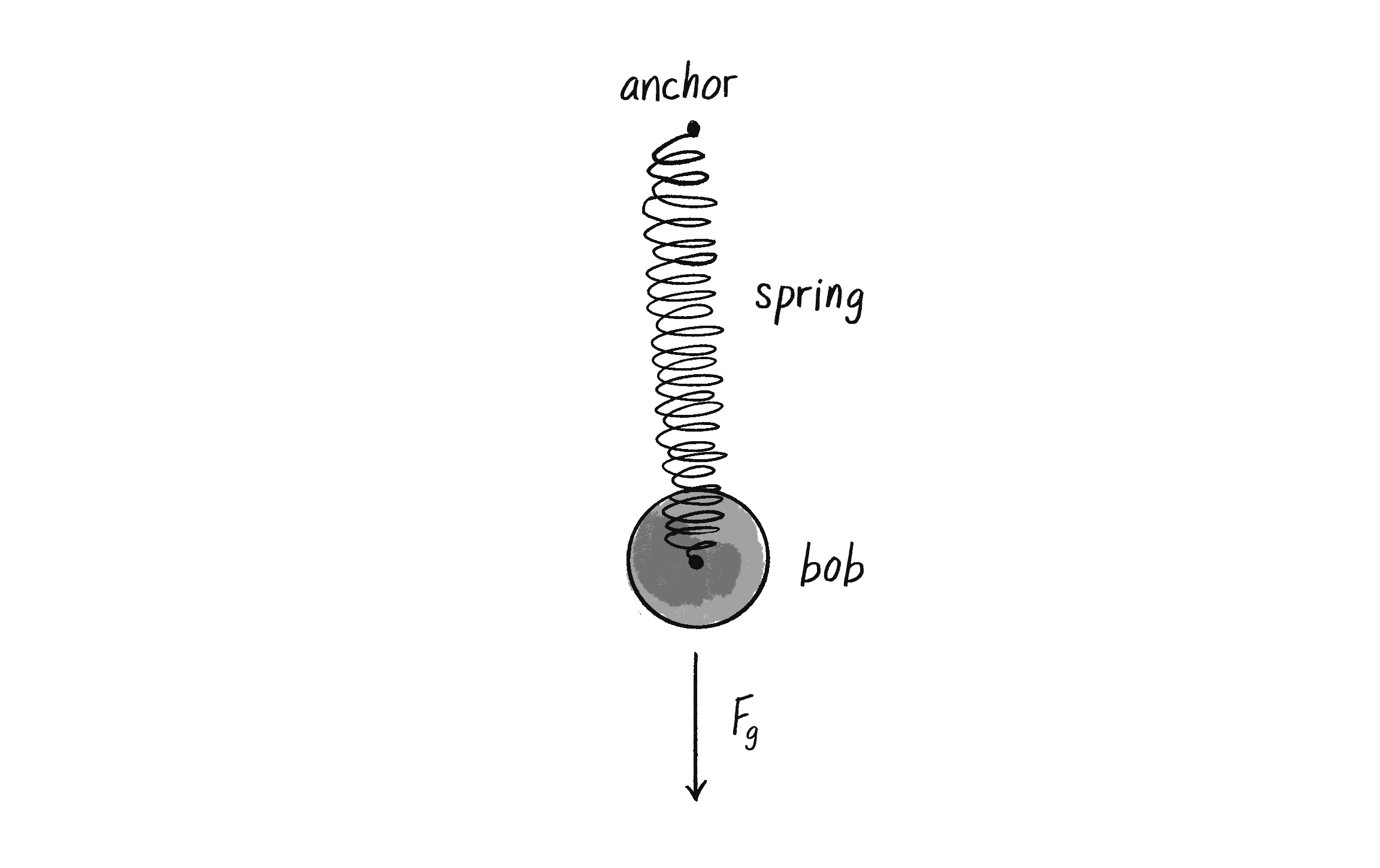
The force of a spring is calculated according to Hooke’s law, named for Robert Hooke, a British physicist who developed the formula in 1660. Hooke originally stated the law in Latin: "Ut tensio, sic vis," or “As the extension, so the force.” Think of it this way:
The force of the spring is directly proportional to the extension of the spring.
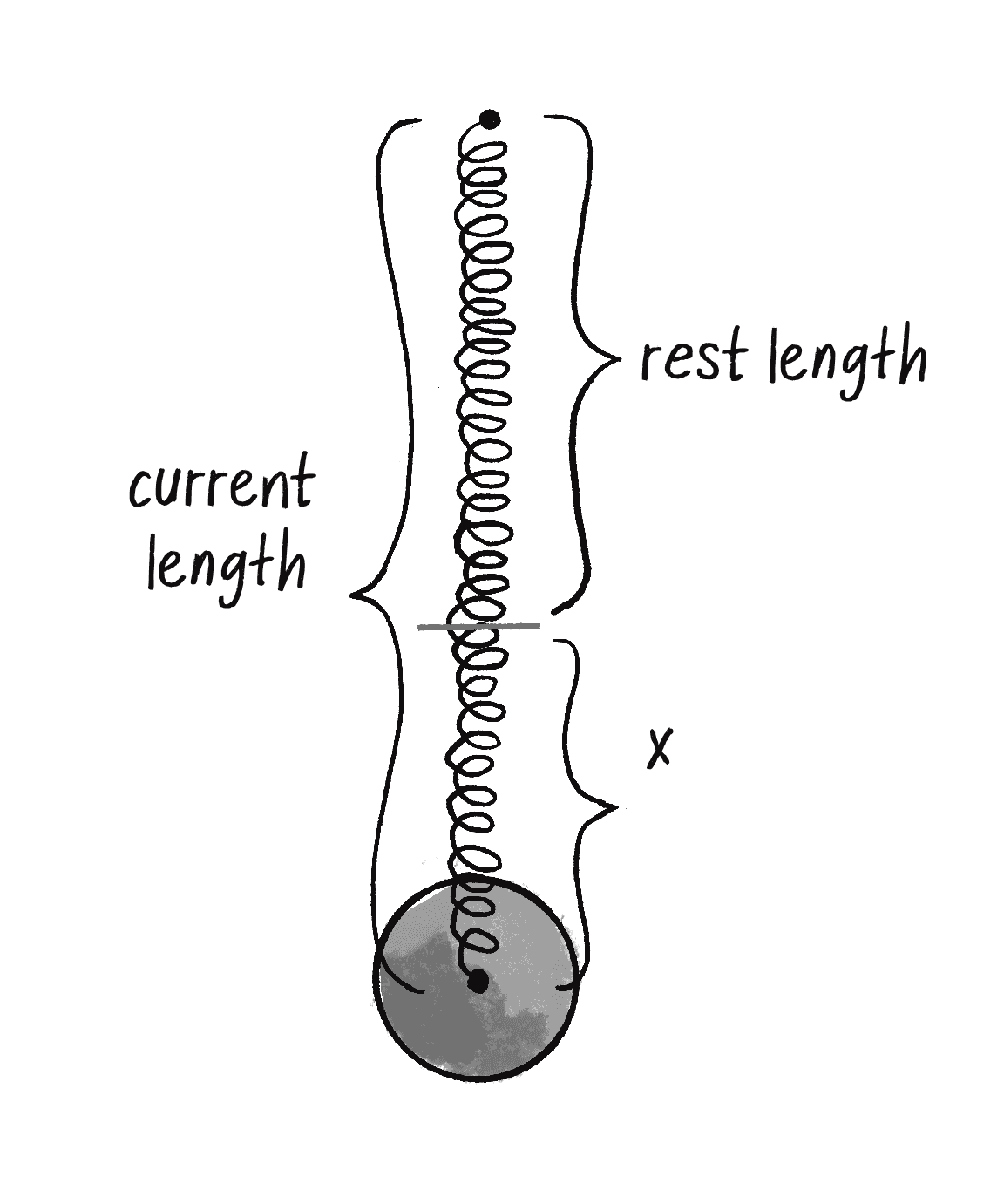
In other words, if you pull on the bob a lot, the force will be strong; if you pull on the bob a little, the force will be weak. Mathematically, the law is stated as follows:
kis constant and its value will ultimately scale the force. Is the spring highly elastic or quite rigid?xrefers to the displacement of the spring, i.e. the difference between the current length and the rest length. The rest length is defined as the length of the spring in a state of equilibrium.
Now remember, force is a vector, so you need to calculate both magnitude and direction. Let’s look at one more diagram of the spring and label all the givens we might have in a p5.js sketch.

For the code, I‘ll start with the following three variables as shown in Figure 3.16.
let anchor = createVector();
let position = createVector();
let restLength = ????;
I’ll then use Hooke’s law to calculate the magnitude of the force. I need to calculate k and x. k is easy; it’s just a constant, so I’ll make something up.
let k = 0.1;
x is perhaps a bit more difficult. I need to know the “difference between the current length and the rest length.” The rest length is defined as the variable restLength. What’s the current length? The distance between the anchor and the bob. And how can I calculate that distance? How about the magnitude of a vector that points from the anchor to the bob? (Note that this is exactly the same process employed when calculating distance in Example 2.9: gravitational attraction.)
let dir = p5.Vector.sub(bob, anchor);
A vector pointing from anchor to bob gives us the current length of the spring.
let currentLength = dir.mag();
let x = currentLength - restLength;
Now that I’ve sorted out the elements necessary for the magnitude of the force (-1 * k * x), I need to figure out the direction, a unit vector pointing in the direction of the force. The good news is that I already have this vector. Right? Just a moment ago I asked the question: “How I can calculate that distance? How about the magnitude of a vector that points from the anchor to the bob?” Well, that is the direction of the force!
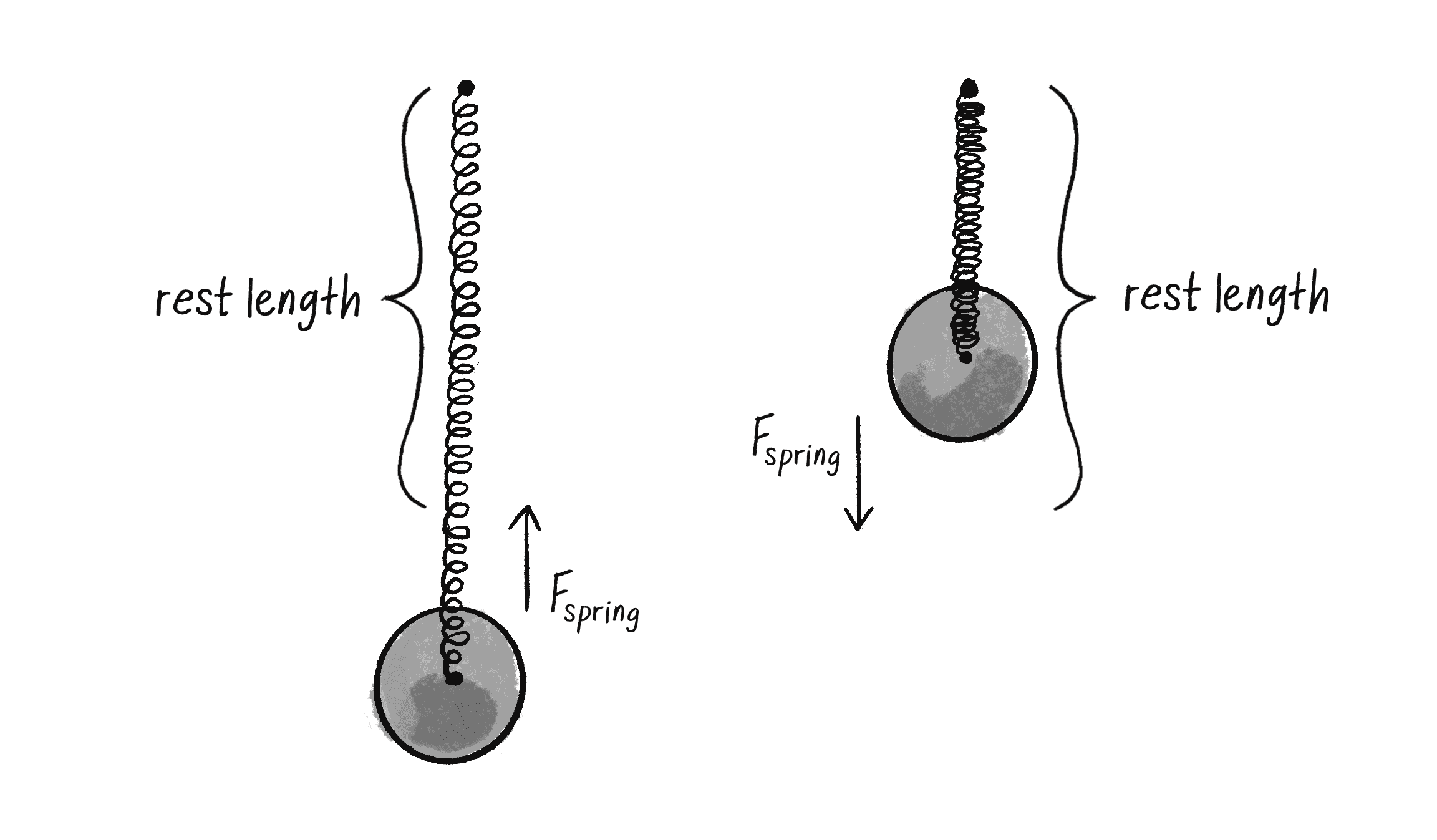
Figure 3.17 shows that if you stretch the spring beyond its rest length, there should be a force pulling it back towards the anchor. And if it shrinks below its rest length, the force should push it away from the anchor. This reversal of direction is accounted for in the formula with the -1. And so all I need to do is set the magnitude of the vector used used for the distance calculation! Let’s take a look at the code and rename that vector variable as force.
let k = 0.1;
let force = p5.Vector.sub(bob, anchor);
let currentLength = force.mag();
let x = currentLength - restLength;
Magnitude of spring force according to Hooke’s law
force.setMag(-1 * k * x);
Putting it together: direction and magnitude!
Now that I have the algorithm worked out for computing the spring force vector, the question remains: what object-oriented programming structure should I use? This, again, is one of those situations in which there is no “correct” answer. There are several possibilities; which one I choose depends on my goals and personal coding style. Since I’ve been working all along with a Mover class, I’ll stick with this same framework. I’ll think of the Mover class as the spring’s “bob.” The bob needs position, velocity, and acceleration vectors to move about the screen. Perfect—I’ve got that already! And perhaps the bob experiences a gravity force via the applyForce() function. Just one more step—applying the spring force:
let bob;
function setup() {
bob = new Bob();
}
function draw() {
let gravity = createVector(0, 1);
Chapter 2 “make-up-a-gravity force”
bob.applyForce(gravity);
let springForce = _______________????
bob.applyForce(spring);
I need to also calculate and apply a spring force!
bob.update();
bob.display();
The standard update() and display() functions
}
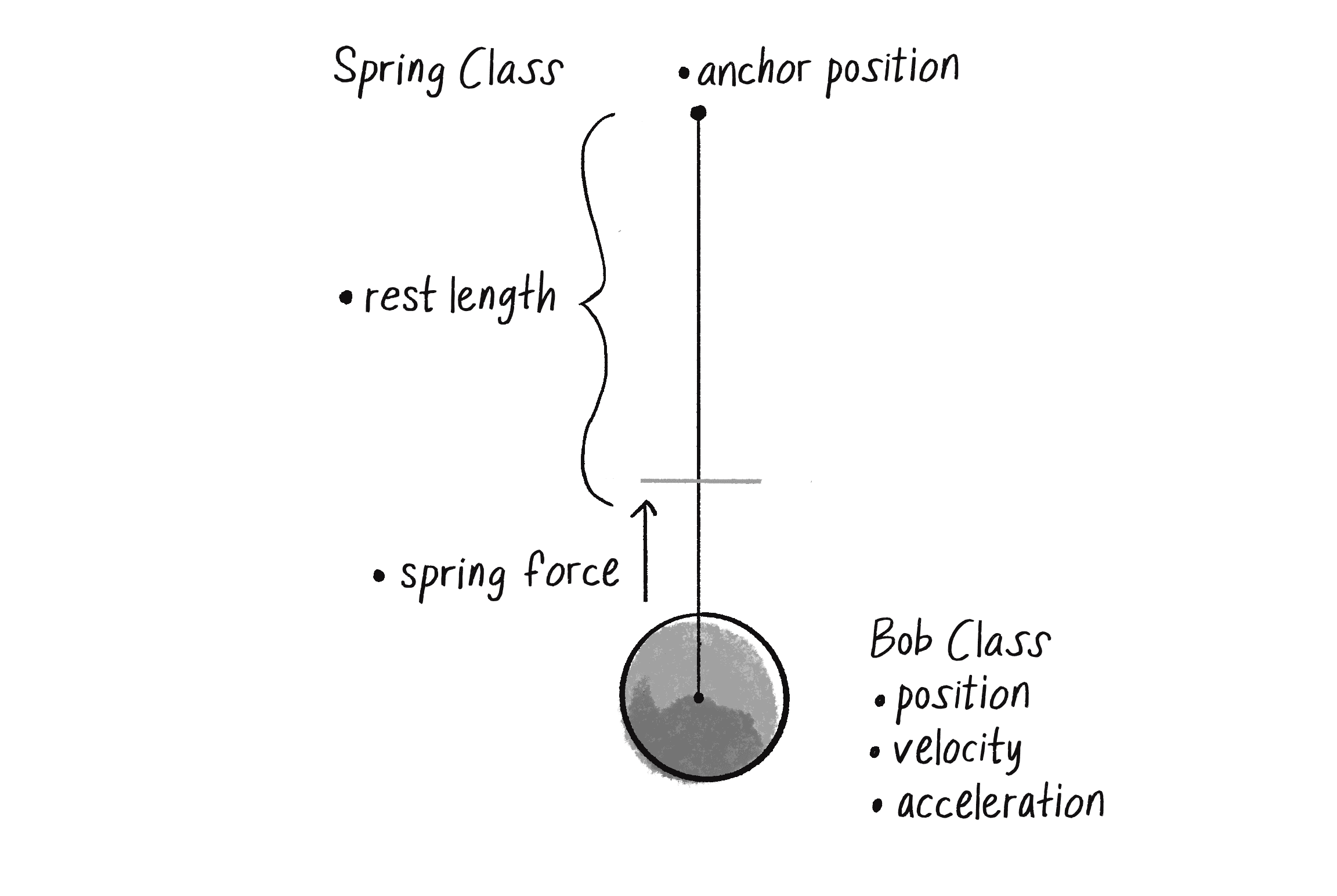
One option would be to write out all of the spring force code in the main draw() loop. But thinking ahead to when you might have multiple bobs and multiple spring connections, it makes a good deal of sense to write an additional class, a Spring class. As shown in Figure 3.18, the Bob class keeps track of the movements of the bob; the Spring class keeps track of the spring’s anchor and its rest length and calculates the spring force on the bob.
This allows me to write a lovely sketch as follows:
let bob;
let spring;
Adding a Spring object
function setup() {
bob = new Bob();
spring = new Spring();
}
function draw() {
let gravity = createVector(0,1);
bob.applyForce(gravity);
spring.connect(bob);
This new function in the Spring class will take care of computing the force of the spring on the bob.
bob.update();
bob.display();
spring.display();
}
You may notice here that this is quite similar to what I did in Example 2.6 with an attractor. There, I wrote something like:
let force = attractor.attract(mover);
mover.applyForce(force);
The analogous situation here with a spring would be:
let force = spring.connect(bob);
bob.applyForce(force);
Nevertheless, in this example all I said was:
spring.connect(bob);
What gives? Why don’t I need to call applyForce() on the bob? The answer is, of course, that I do need to call applyForce() on the bob. Only instead of doing it in draw(), I’m demonstrating that a perfectly reasonable (and sometimes preferable) alternative is to ask the connect() function to internally handle calling applyForce() on the bob.
connect(bob) {
let force = some fancy calculations
bob.applyForce(force);
The function connect() takes care of calling applyForce() and therefore doesn’t have to return a vector to the calling area.
}
Why do it one way with the Attractor class and another way with the Spring class? When I first discussed forces, it was a bit clearer to show all the forces being applied in the draw() loop, and hopefully this helped you learn about force accumulation. Now that you’re more comfortable with that, perhaps it’s simpler to embed some of the details inside the objects themselves.
Let’s take a look at the rest of the elements in the Spring class.
Example 3.11: A Spring connection
class Spring {
constructor(x, y, length) {
The constructor initializes the anchor point and rest length.
this.anchor = createVector(x, y);
The spring’s anchor position.
this.length = length;
this.k = 0.1;
Rest length and spring constant variables
}
connect(bob) {
Calculate spring force—our implementation of Hooke’s Law.
let force = p5.Vector.sub(bob.position, this.anchor);
Get a vector pointing from anchor to Bob position.
let d = force.mag();
let stretch = d - this.length;
Calculate the displacement between distance and rest length.
force.normalize();
force.mult(-1 * this.k * stretch);
Direction and magnitude together!
bob.applyForce(force);
Call applyForce() right here!
}
display() {
fill(100);
circle(this.anchor.x, this.anchor.y, 10);
}
Draw the anchor.
displayLine(b) {
stroke(255);
line(b.position.x, b.position.y, this.anchor.x, this.anchor.y);
}
Draw the spring connection between Bob position and anchor.
}
The full code for this example is included on the book website, and the that version also incorporates two additional features: (1) the Bob class includes functions for mouse interactivity so that the bob can be dragged around the window, and (2) the Spring object includes a function to constrain the connection’s length between a minimum and a maximum.
Exercise 3.15
Before running to see the example online, take a look at this constrain function and see if you can fill in the blanks.
constrainLength(b, minlen, maxlen) {
let dir = p5.Vector.sub(______,______);
Vector pointing from Bob to Anchor
let d = dir.mag();
if (d < minlen) {
Is it too short?
dir.setMag(________);
b.position = p5.Vector.add(______, ______);
Keep position within constraint.
b.velocity.mult(0);
} else if (____________) {
Is it too long?
dir.setMag(_________);
b.position = p5.Vector.add(______, ______);
Keep position within constraint.
b.velocity.mult(0);
}
}
Exercise 3.16
Create a system of multiple bobs and spring connections. Try connecting a bob to another bob with no fixed anchor?
The Ecosystem Project
Step 3 Exercise:
Take one of your creatures and incorporate oscillation into its motion. You can use the Oscillator class from Example 3.7 as a model. The Oscillator object, however, oscillates around a single point (the middle of the window). Try oscillating around a moving point. In other words, design a creature that moves around the screen according to position, velocity, and acceleration. But that creature isn’t just a static shape, it’s an oscillating body. Consider tying the speed of oscillation to the speed of motion. Think of a butterfly’s flapping wings or the legs of an insect. Can you make it appear that the creature’s internal mechanics (oscillation) drive its locomotion? For a sample, check out the “AttractionArrayWithOscillation” example with the code download.
let angle = 60; rotate(radians(angle)); angleMode(DEGREES); rotate(angle);